In the fall of 2021, a friend who runs her own business sent me this picture with the accompanying question:
The screenshot indicates an average1 rating of 4.5 stars out of a total of \(n = 363\) reviews, and additionally lists the percent of time a rating between 1-5 was given.
1 Unweighted, I assume.
It seemed like an easy enough problem – perfect to explore on a rainy, gray Saturday in November – so I decided to have a crack at it.
After doing some trivial algebra, somewhat successfully writing a for-loop, and adequately pleased with the solution, I posted the write-up for my initial approach on RPubs and sent off the answer2 to my friend.
2 Spoiler: she needed between 47-50 5-star ratings to pull up the average rating to 4.6. Apologies if you were eagerly waiting for the end to find out what the answer was.
However, while going through this document to clean it up for the blog (in 2022), I realized there’s a simpler way of solving this problem. Before I describe it further, I’m going to load some R packages and extract the data from the image into R objects.
library(purrr)library(tidyr)library(dplyr)
Attaching package: 'dplyr'
The following objects are masked from 'package:stats':
filter, lag
The following objects are masked from 'package:base':
intersect, setdiff, setequal, union
n <-363# percent ratings scaled to [0,1]p <-c(0.06, 0.01, 0.02, 0.12, 0.79) %>%set_names(nm =1:5) %>%print()
1 2 3 4 5
0.06 0.01 0.02 0.12 0.79
What made me rethink my approach was that I previously ended up with the wrong ratings vector after converting the (rounded) percentages into counts3.
3 Although I mostly worked around it afterwards via simulation.
So for example, 79% out of 363 ratings were 5-star ratings, which translates to 286.77 and rounded to the nearest integer becomes 287. But this isn’t the only integer that rounds to 79% when divided by 363. Any integer \(k\) when divided by 363 that ends up in the (open) interval (78.5%, 79.5%) would be a possible candidate.
So any one of 285-288 5-star ratings are compatible with the information in the screenshot. We can get the same range for the other ratings (i.e., 1-4).
plausible_counts_per_rating <- p %>%map(.f =function(prop) { approx_val <-round(prop * n) possible_vals <-seq(from = approx_val -10, to = approx_val +10, by =1) %>%set_names(nm =~ .x) %>%map_dbl(.f =~round(.x / n, 2)) %>%keep(.p =~ .x == prop) %>%names()}) %>%as_tibble(.name_repair =~paste('x', .x, sep =""))plausible_counts_per_rating
Each column shows the plausible values for the number of times a rating was provided. We can create all possible combinations of these values to identify the subset of \(4 ^ 5 = 1024\) possible combinations that are compatible with the information in the screenshot, i.e., a mean of 4.5 when rounded to 1 decimal place and a total of 363 ratings.
Warning: There was 1 warning in `mutate()`.
ℹ In argument: `across(.fns = as.integer)`.
Caused by warning:
! Using `across()` without supplying `.cols` was deprecated in dplyr 1.1.0.
ℹ Please supply `.cols` instead.
So one of these three possible vectors is used to produce the statistics shown in the screenshot.
The formula for computing the (arithmetic) mean can be rearranged to easily calculate the required number of five-star ratings to bring the mean from 4.5 to 4.6.
Let \(n_1\) denote the number of additional five-star ratings, \(y\) the (weighted) sum of the rating counts, and \(n\) the current number of ratings (i.e., 363) in the following equation:
so 47-50 additional 5-star ratings are needed to pull up the average4 to 4.6, assuming that the future ratings are all five-star ratings.
4 exact average, not an average resulting from rounding 4.57 (say) to 4.6. In the latter case, fewer than 47 five-star ratings would be required.
Source Code
---title: "How Many Five-Star Ratings Do I Need?"date: "2022-08-16"categories: [Analysis, Miscellaneous, R]toc: falsecode-fold: falsereference-location: margin---In the fall of 2021, a friend who runs her own business sent me this picture with the accompanying question: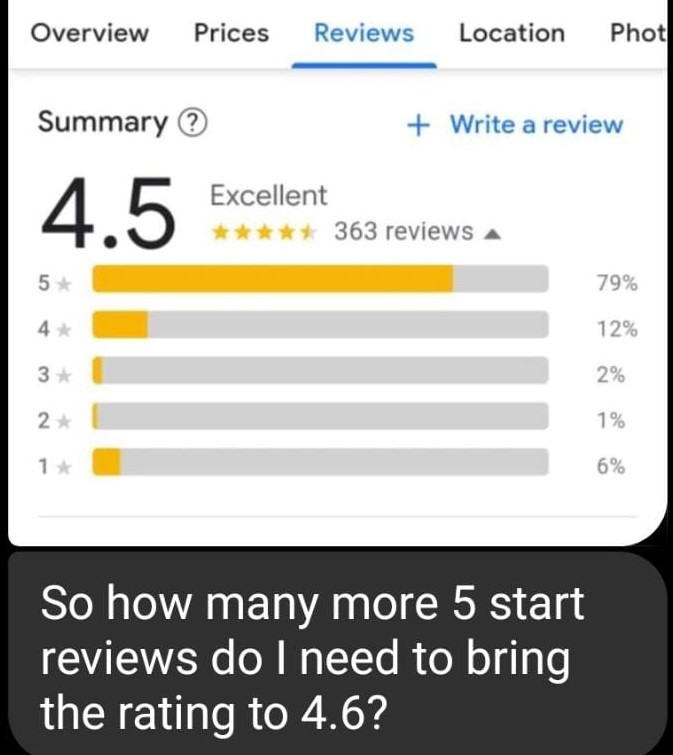The screenshot indicates an average[^1] rating of 4.5 stars out of a total of $n = 363$ reviews, and additionally lists the percent of time a rating between 1-5 was given.[^1]: Unweighted, I assume.It seemed like an easy enough problem -- perfect to explore on a rainy, gray Saturday in November -- so I decided to have a crack at it.After doing some trivial algebra, somewhat successfully writing a for-loop, and adequately pleased with the solution, I posted the write-up for my initial approach on [RPubs](https://rpubs.com/akshatdwivedi/five-star-ratings) and sent off the answer[^2] to my friend.[^2]: Spoiler: she needed between 47-50 5-star ratings to pull up the average rating to 4.6. Apologies if you were eagerly waiting for the end to find out what the answer was.However, while going through this document to clean it up for the blog (in 2022), I realized there's a simpler way of solving this problem. Before I describe it further, I'm going to load some R packages and extract the data from the image into R objects.```{r}library(purrr)library(tidyr)library(dplyr)n <-363# percent ratings scaled to [0,1]p <-c(0.06, 0.01, 0.02, 0.12, 0.79) %>%set_names(nm =1:5) %>%print()```What made me rethink my approach was that I previously ended up with the wrong ratings vector after converting the (rounded) percentages into counts[^3].[^3]: Although I mostly worked around it afterwards via simulation.So for example, 79% out of 363 ratings were 5-star ratings, which translates to `r p[5] * n` and rounded to the nearest integer becomes `r round(p[5] * n)`. But this isn't the only integer that rounds to 79% when divided by `r n`. Any integer $k$ when divided by `r n` that ends up in the (open) interval (78.5%, 79.5%) would be a possible candidate.```{r}seq(284, 289, 1) %>%set_names(nm =~ .x) %>%map_dbl(.f =~round(100* .x /363))```So any one of 285-288 5-star ratings are compatible with the information in the screenshot. We can get the same range for the other ratings (i.e., 1-4).```{r}plausible_counts_per_rating <- p %>%map(.f =function(prop) { approx_val <-round(prop * n) possible_vals <-seq(from = approx_val -10, to = approx_val +10, by =1) %>%set_names(nm =~ .x) %>%map_dbl(.f =~round(.x / n, 2)) %>%keep(.p =~ .x == prop) %>%names()}) %>%as_tibble(.name_repair =~paste('x', .x, sep =""))plausible_counts_per_rating```Each column shows the plausible values for the number of times a rating was provided. We can create all possible combinations of these values to identify the subset of $4 ^ 5 = 1024$ possible combinations that are compatible with the information in the screenshot, i.e., a mean of 4.5 when rounded to 1 decimal place and a total of 363 ratings.```{r}rating_combinations <- plausible_counts_per_rating %>%# create all combinations of all values in all columnsexpand(crossing(x1, x2, x3, x4, x5)) %>%mutate(across(.fns = as.integer), total_ratings = x1 + x2 + x3 + x4 + x5, sum_ratings = x1 + (2* x2) + (3* x3) + (4* x4) + (5* x5), mean_rating =round(sum_ratings /363, 1)) %>%print(n =10)``````{r}possible_ratings <- rating_combinations %>%filter(total_ratings ==363, mean_rating ==4.5) %>%print(n =Inf)```So one of these three possible vectors is used to produce the statistics shown in the screenshot.The formula for computing the (arithmetic) mean can be rearranged to easily calculate the required number of five-star ratings to bring the mean from 4.5 to 4.6.Let $n_1$ denote the number of additional five-star ratings, $y$ the (weighted) sum of the rating counts, and $n$ the current number of ratings (i.e., `r n`) in the following equation:$$\frac{y + (n_1 \times 5)}{n + n_1} = 4.6$$This can be rewritten as$$5n_1 = 4.6 \times (n + n_1) - y$$and simplified to yield$$n_1 = \frac{(4.6 \times n) - y}{0.4}$$and coded up as an R function```{r}num_five_star <-function(sum_ratings, total_ratings) { ((4.6* total_ratings) - sum_ratings) /0.4}```Applying this function to the possible ratings vector leads to```{r}possible_ratings %>%mutate(extra_5_stars =ceiling(num_five_star(sum_ratings, total_ratings))) %>%select(-total_ratings, -mean_rating)```so 47-50 additional 5-star ratings are needed to pull up the average[^4] to 4.6, assuming that the future ratings are all five-star ratings.[^4]: exact average, not an average resulting from rounding 4.57 (say) to 4.6. In the latter case, fewer than 47 five-star ratings would be required.